词法分析器

RE，NFA，DFA的关系

RE到NFA：Thompson构造法。就是每种正则表达式的基本构造（\(ab\)，\(a\vert b\)，\(a\ast b\)）都有对应的NFA的模板。
NFA到DFA：子集构造法。就是从集合\(\{n_0\}\)开始，将其\(\epsilon{-}closure\)作为一个所求DFA的状态；然后把每个这样得到的状态在经过\(\Sigma\)上每个字符转移后得到的集合的\(\epsilon{-}closure\)也作为新的状态；直到没有新的状态为止。
最小化DFA：Hopcroft算法。一开始把初始结点作为一个集合，除初始结点外的其他结点作为另一个集合。每次从已有集合选出一个，判断是否有\(\Sigma\)上的字符可以将该集合分成两组，使得该两组集合经过该字符转以后到达不同的已有集合。如果是，就把该集合替换为该两个新集合。直到没有更多的拆分为止。最后每个集合作为所求DFA的一个状态。

如何证明正确性？
最小化DFA的另一种算法：直接从NFA构造最小DFA的Brzozowski算法。观察得知：子集构造法总是生成不包含重复前缀路径的DFA

如何证明？

根据这种观察，我们令：
- \(reverse(n)\)是NFA \(n\)经过这些操作得到的NFA：翻转\(n\)中所有转移的方向，将初始状态设为\(reverse(n)\)的接受状态，增加一个新的初始状态，将其通过\(\epsilon\)边连接到\(n\)中所有的接受状态
- \(reachable(n)\)返回NFA \(n\)中从初始状态可到达的状态和转移的集合（即删掉不可达状态和转移后的子NFA）
- \(subset(n)\)为对\(n\)应用子集构造法生成的DFA
- 这样，给定NFA \(n\)，等价的最小DFA就是下述表达式：\(reachable(subset(reverse(reachable(subset(reverse(n))))))\)
  
  如何证明？而且有何实际意义？
DFA到RE：Kleen构造法。基本思想：DFA是一个图，如果图无环，构造算法是显然的：枚举所有路径即可（路径数量有限）；如果有环，可能的环的种类也是有限的，通过RE的闭包运算可以模拟这些环。
- 上述算法中，\(R_{ij}^k\)描述了DFA中从状态\(i\)到状态\(j\)、不经由编号大于\(k\)的状态的所有路径。这里“经由”表示“进入且离开”。

词法分析器

表驱动的词法分析器
- 识别token的基本算法
- 上述算法会导致平方级别的回滚调用。考虑正则表达式\(ab\vert(ab)\ast c\)，对于串\(abababab\)会导致平方级别回滚，因为在读到终结符前都不会到达\(s_e\)。下面改进的算法通过保存额外的失败信息可以避免这个问题。基本思想就是找出上面算法中在重复过去相同的回滚时所做的重复计算，然后把这些重复计算的结果在第一次计算时就保存下来：
直接编码的词法分析器：降低了计算DFA转移的成本，将原本显式表示的DFA状态和转移图替换为隐式表示方法。即：把转移实现为函数调用，对每个不同的状态都有一个单独的\(NextChar()\)函数与之对应，每个函数内都编码了如\(lexeme\gets lexeme+char\)的操作，因此代码有很多重复
手工编码的词法分析器：对直接编码的词法分析器高度优化以减少分析器和系统其余组件之间的接口的开销

语法分析器

各种语言和语法分析器

各个语言的包含关系：\(RG(Regular Grammar)\subset LL(1)\subset LR(1)\subset CFG(Context Free Grammar)\)
- 任意CFG需要花费更多的时间进行语法分析。如Earley算法可以在\(O(n^3)\)时间内解析任意CFG
- LR(1)语法包含了无歧义CFG的很大一个子集，可以在线性时间内扫描输入并自底向上进行语法分析，任何时候都只需从当前输入符号前瞻最多一个单词
- LL(1)可以在线性时间内扫描输入并自顶向下（通过手工编码的递归下降分析器或生成的LL(1)分析器）进行语法分析，只需前瞻一个单词
自顶向下的语法分析
- 自顶向下的语法分析可以高效进行的一个关键点是：上下文无关语法的很大一个子集不进行回溯即可以完成语法分析
最左（右）推导：一种推导，在每个步骤多重写最左（右）侧的非终结符。最左和最右推导运用产生式的顺序不同。但因为语法分析树只表示应用了那些规则，而未指定按何种顺序应用规则，因此，对于无歧义语法来说，两种推导得出的语法分析树是相同的

自顶向下语法分析：无回溯语法

自顶向下语法分析器可能会无限循环（因为左递归）。很容易消除直接左递归（略），消除间接左递归的算法如下（将间接左递归转换为直接左递归，再重写直接左递归为右递归）：
解决了无限循环问题后还是有可能会回溯。可以利用一个简单修改来（尝试）避免回溯：在选择下一条产生式时，可以同时考虑当前关注的符号以及下一个输入符号（前瞻符号）。如果这样做后不需要回溯，就说该语法在前瞻一个符号时是无回溯的。形式化定义如下：
- \(FIRST(\alpha)\)定义为语法符号（可以为终结符\(T\)或非终结符\(NT\)）\(\alpha\)推导出的语句开头可能出现的终结符的集合。\(\epsilon\)和\(eof\)同时出现在\(FIRST\)的定义域和值域中。可以通过一个简单的不动点算法算出每个语法符号的\(FIRST\)集合，如下：
- 当前瞻符号不是任何其他备选产生式的\(FIRST\)集合的成员，且存在形如\(A\to\epsilon\)的产生式时，应该使用该\(\epsilon\)产生式。但为了区分合法输入和语法错误，语法分析器必须知道在应用了该产生式后哪些单词可能作为第一个符号出现。为此定义\(FOLLOW(\alpha)\)为紧跟非终结符\(\alpha\)导出的符号串之后的所有可能单词，计算方法如下：
- 为准确定义无回溯条件，对于产生式\(A\to\beta\)，定义其增强\(FIRST\)集\(FIRST^+\)，如下
  \[FIRST^+(A\to\beta)=\left\{ \begin{array}{l} FIRST(\beta)\ \textbf{if}\ \epsilon\notin FIRST(\beta)\\ FIRST(\beta)\cup FOLLOW(A)\ \textbf{otherwise} \end{array} \right.\]
  这样，一个语法是无回溯语法的充分条件是，对任何匹配多个产生式的非终结符\(A\)，\(A\to\beta_1\vert\beta_2\vert\cdots\beta_n\)，有
  \[FIRST^+(A\to\beta_i)\cap FIRST^+(A\to\beta_j)=\emptyset, \forall 1\le i,j\le n, i\ne j\]
一个有回溯的语法有时可以通过提取左因子（left factoring，即提取并隔离共同前缀的过程）将其变为无回溯语法
然而某些上下文无关语言没有无回溯语法。一般来说，对于任意的上下文无关语言，是否存在无回溯语法是不可判定的。

如何证明？
有时候前瞻两个符号也可以解决回溯的问题，但是对于使用任意有限个前瞻符号的情况，都可以设计出一种语法，使得在给定数目的前瞻符号下不足以进行预测

自顶向下语法分析：递归下降法

实现的方法就是，为每个非终结符实现一个函数（类似于直接编码的DFA词法分析器），根据前瞻符号来决定使用哪个产生式，根据选择的产生式中的非终结符再调用对应的函数。

自顶向下语法分析：表驱动的LL(1)语法分析器

LL(1)：由左（Left，L）向右扫描输入，构建一个最左推导（Leftmost，L），其中仅使用一个前瞻符号（1）。根据定义，LL(1)是无回溯的，因此其只能接受右递归、无回溯的语法。
算法：
生成上述算法中的LL(1)表\(Table\)的算法：
如果语法不是无回溯的，上述构建将对\(Table\)表中的某些元素分配多个产生式

自底向上语法分析

一些名词：
- 上边缘：自底向上语法分析会构建一棵部分完成的语法分析树，其实质是一个森林，可以有多个树根。这些根节点的列（上边）的右侧边缘（缘）称为上边缘。
- LR(1)的特点：从左（Left）到右扫描，反向（Reverse）最右推导，一个（1）前瞻符号
- 为什么是反向最右推导而不是最左（注意对于无歧义文法最左和最右推导得到的语法树是一样的，因此这里考虑的只是推导的顺序，即为什么是按照反向最右推导的顺序）：因为归约发生在语法分析树的上边缘（右侧），此时左边的子树（子森林）已经归约完成，因此右侧子树是最后归约的，那么将整个顺序反过来就变为，最右侧的子树是最早推导的，即最右推导的定义。
- LR语法（指LR(k)）分析技术可以用来分析很大一类（但不是全部）无歧义语法
- 句柄是一个对\(\langle A\to\beta,k\rangle\)，其中\(\beta\)出现在语法分析树的上边缘，而其右侧末端位于位置\(k\)，且将\(\beta\)替换为\(A\)是语法分析中的下一步
- LR语法分析器中，句柄总是位于栈顶（见下面算法），而各个句柄的链构成了一个反向的最右推导
- 增加的前瞻符号并不能增大LR语法分析器可以识别的语言集合。对于\(k>1\)，LR(1)语法分析器与LR(k)语法分析器接受的语言集合是相同的。但是，同一语言的LR(1)语法可能比LR(k)语法更复杂。
LR(1)算法：
构建\(Action\)表和\(Goto\)表
- LR(1)项：形如\([A\to\beta\cdot\gamma,a]\)，其中\(A\to\beta\gamma\)是一个产生式，\(\cdot\)表示语法分析器栈顶的位置，而\(a\)是语法中的一个终结符。这个项表示，语法分析器已经从\([A\to\cdot\beta\gamma,a]\)（另一个LR(1)项）前进了一步（识别了\(\beta\)），如果输入确实能归约到\(A\)，下一步将要识别出\(\gamma\)；而这里\(a\)表示，\(A\)后接\(a\)是符合语法的，即如果在识别了\(\gamma\)后前瞻符号为\(a\)，语法分析器可以将\(\beta\gamma\)归约到\(A\)。
- 为简化任务，要求语法有一个唯一的目标符号（非终结符），该符号不会出现在任一产生式的右侧。设该符号为\(S'\)，则\(\{[S'\to S, eof]\}\)形成了LR(1)项集的规范族CC的第一个状态\(CC_0\)的核心项集。下面的闭包运算可以根据此核心项集计算出\(CC_0\)的完备项集。
- LR(1)项集合的两个基本运算：
  - 闭包运算：
  - goto过程实现了语法分析器根据当前状态和某个语法符号进行的转移过程。
- 构建LR(1)项集的规范族CC：
- 构建\(Action\)表和\(Goto\)表：
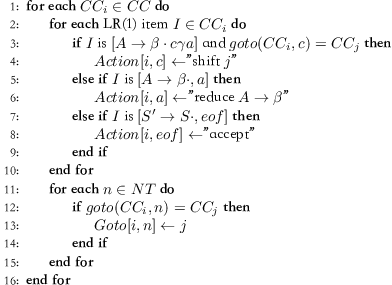
一些观察：LR(1)语法分析器的效率，来源于\(Action\)表和\(Goto\)表内蕴的快速句柄查找机制。规范族CC表示了一个句柄查找DFA（局病毒集合是有限的，因此句柄的语言是一种正则语言）